

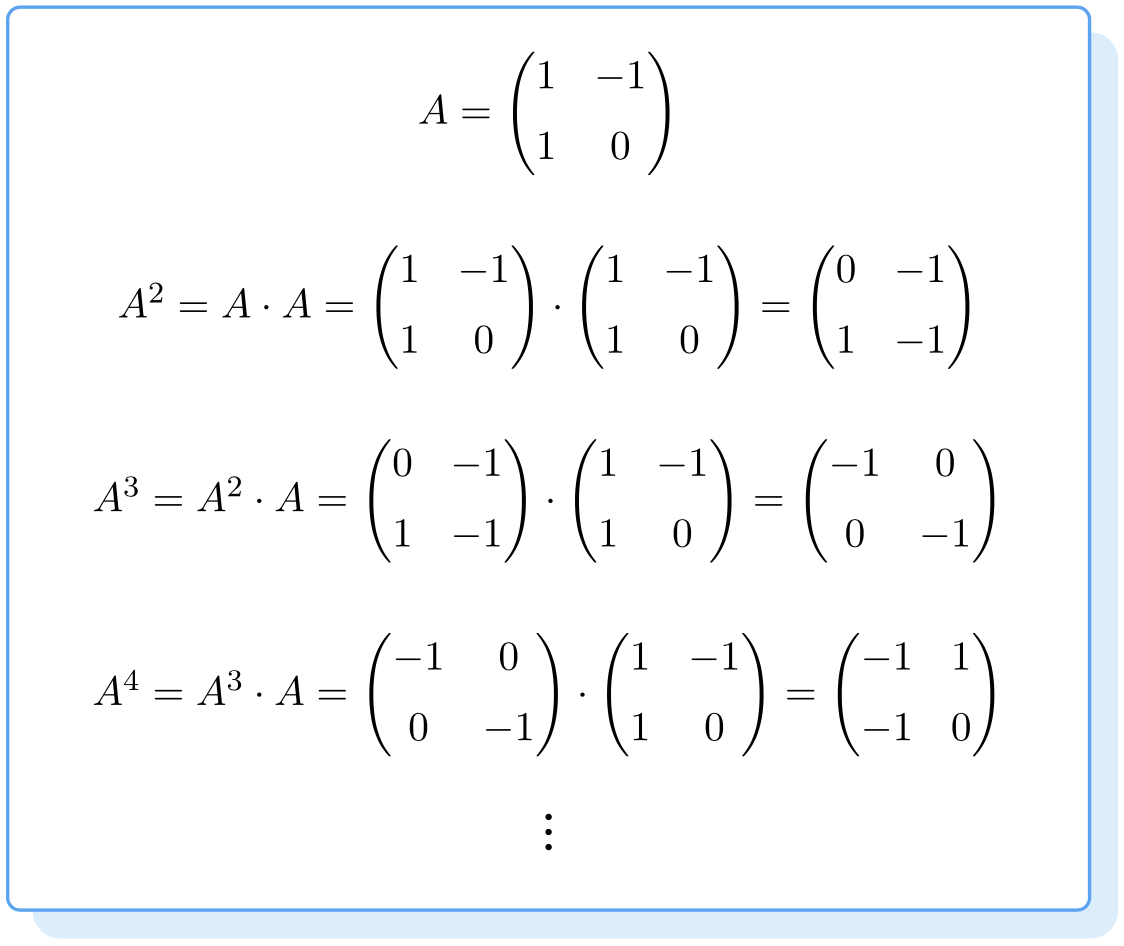
For instance, in an academic collaboration network, the similarity between two authors can be defined as the number of papers that the authors published together. In network clustering, the similarity function is typically defined in terms of the topology of the network. The first step in network clustering is the definition of a similarity function between nodes. Network clustering is an organization process with the goal to put similar nodes together the result is a partition of the network into a set of communities. The distribution for closeness resembles a normal curve, while the other centrality measures have a long tail distribution similar to a power law.Ī typical group-level analysis is network clustering. Hist(btwcent, breaks=30, main="Betweenness centrality", xlab="Betweenness") Hist(clocent, breaks=30, main="Closeness centrality", xlab="Closeness") Hist(eigcent, breaks=30, main="Eigenvector centrality", xlab="Eigenvector") Hist(degcent, breaks=30, main="Degree centrality", xlab="Degree") Let's see how the computed centrality measures are distributed: Moreover, eigenvector centrality is best associated with betweenness centrality, while closeness is the less correlated measure, in particular closeness and betweenness have the lowest correlation coefficient. By contrast, degree centrality has less impact on closeness centrality. Moreover, if a node $x$ has $k$ neighbours, there are $k \cdot (k-1)$ short paths of the form $u_1, x, u_2$, where $u_1$ and $u_2$ are neighbours of $x$, each of them having a good chance of being a geodesic that passes trough $x$. Indeed, the shortest path between the neighbours of a node passes through the node unless the neighbour nodes are directly connected. In particular, notice how nodes with a high degree have also a high betweenness centrality. Not surprisingly, the four centrality measures are positively correlated. M = cbind(degcent, eigcent, clocent, btwcent)
G = barabasi.game(1000, m = 2, directed=FALSE, out.pref = TRUE) Let's check the correlation between the four centrality measures on a random scale-free network: Brandes devised an algorithm for unweighted graphs that requires $O(n+m)$ space and run in $O(nm)$ time. On sparse graphs, Johnson algorithm is more efficient, taking $O(n^2 \log n + nm)$. If the graph has $n$ nodes and $m$ edges, this takes $O(n^3)$ time with Floyd-Warshall algorithm. Plot(g, layout=coords, vertex.label=round(clocent, 2))Ĭalculating closeness and betweenness centrality for all nodes in a graph involves computing the shortest paths between all pairs of nodes in the graph. If we view a network edge as a channel where information flows, then nodes with large closeness scores can access information very quickly from other nodes and similarly can rapidly spread information to the other nodes.įunction closeness computes closeness centrality: For instance, if a node is directly connected to each other node, then its closeness is 1, while an isolated node has closeness equal to $1 / n$. If there is no path between nodes $i$ and $j$ then the total number $n$ of vertices is used in the formula instead of the path length.Ĭloseness lies in the interval $$: nodes with closeness approaching 1 are nodes with short distance from the other nodes, while nodes with low closeness are distant from the other nodes. Where $d(i,j)$ is the geodesic distance between nodes $i$ and $j$ and $n$ is the number of nodes of the graph. Let $L$ be the adjacency matrix of a graph, that is, $l_$ The simplest of centrality measure is degree centrality. Element-level analysisĬentrality measures are indicators of the importance (status, prestige, standing, and the like) of a node in a network. All network properties, however, can be generalized to directed as well as weighted graphs. In the following we will focus on undirected unweighted graphs. network-level analysis, that focuses on topological properties of networks as a whole.group-level analysis, that involves methods for defining and finding cohesive groups of nodes in the network, and.element-level analysis, where methods to identify the most important nodes of the network are investigated,.Network analysis studies properties at three levels of abstraction: Besides solving the riddle, Euler unintentionally showed that networks have properties, which dependent on their topological architecture, that limit or enhance their usability.

Euler is credited as the father of graph theory and the Köningsberg bridge network as the first example of a graph.


 0 kommentar(er)
0 kommentar(er)
